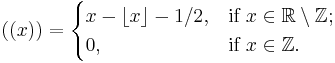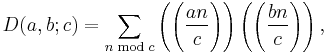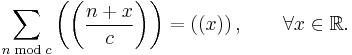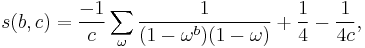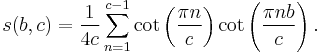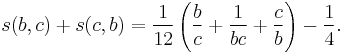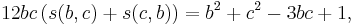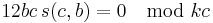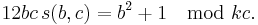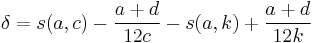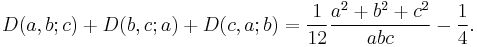Dedekind sum

In mathematics, Dedekind sums, named after Richard Dedekind, are certain sums of products of a sawtooth function, and are given by a function D of three integer variables. Dedekind introduced them to express the functional equation of the Dedekind eta function. They have subsequently been much studied in number theory, and have occurred in some problems of topology. Dedekind sums obey a large number of relationships on themselves; this article lists only a tiny fraction of these.

Contents

Definition

Define the sawtooth function 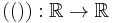\left( \left( \right) \right):\mathbb{R} \rightarrow \mathbb{R} as

((x))=\begin{cases} x-\lfloor x\rfloor - 1/2, &\mbox{if }x\in\mathbb{R}\setminus\mathbb{Z};\\ 0,&\mbox{if }x\in\mathbb{Z}. \end{cases}

We then let

D :Z3 → R

be defined by

D(a,b;c)=\sum_{n \bmod c} \left( \Bigg( \frac{an}{c} \Bigg) \right) \left( \left( \frac{bn}{c} \right) \right),

the terms on the right being the Dedekind sums. For the case a=1, one often writes

s(b,c) = D(1,b;c).

Simple formulae

Note that D is symmetric in a and b, and hence

D(a,b;c)=D(b,a;c),

and that, by the oddness of (()),

D(−a,b;c) = −D(a,b;c),
D(a,b;−c) = D(a,b;c).

By the periodicity of D in its first two arguments, the third argument being the length of the period for both,

D(a,b;c)=D(a+kc,b+lc;c), for all integers k,l.

If d is a positive integer, then

D(ad,bd;cd) = dD(a,b;c),
D(ad,bd;c) = D(a,b;c), if (d,c) = 1,
D(ad,b;cd) = D(a,b;c), if (d,b) = 1.

There is a proof for the last equality making use of

\sum_{n \bmod c} \left( \left( \frac{n%2Bx}{c} \right) \right)=\left(\left( x\right)\right),\qquad\forall x\in\mathbb{R}.

Furthermore, az = 1 (mod c) implies D(a,b;c) = D(1,bz;c).

Alternative forms

If b and c are coprime, we may write s(b,c) as

s(b,c)=\frac{-1}{c} \sum_\omega \frac{1} { (1-\omega^b) (1-\omega ) } %2B\frac{1}{4} - \frac{1}{4c},

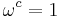where the sum extends over the c-th roots of unity other than 1, i.e. over all \omega such that \omega^c=1 and \omega\not=1.

If b, c > 0 are coprime, then

s(b,c)=\frac{1}{4c}\sum_{n=1}^{c-1} \cot \left( \frac{\pi n}{c} \right) \cot \left( \frac{\pi nb}{c} \right).

Reciprocity law

If b and c are coprime positive integers then

s(b,c)%2Bs(c,b) =\frac{1}{12}\left(\frac{b}{c}%2B\frac{1}{bc}%2B\frac{c}{b}\right)-\frac{1}{4}.

Rewriting this as

12bc \left( s(b,c) %2B s(c,b) \right) = b^2 %2B c^2 -3bc %2B 1,

it follows that the number 6c s(b,c) is an integer.

If k = (3, c) then

12bc\, s(c,b)=0 \mod kc

and

12bc\, s(b,c)=b^2%2B1 \mod kc.

A relation that is prominent in the theory of the Dedekind eta function is the following. Let q = 3, 5, 7 or 13 and let n = 24/(q − 1). Then given integers a, b, c, d with ad − bc = 1 (thus belonging to the modular group), with c chosen so that c = kq for some integer k > 0, define

\delta = s(a,c) - \frac{a%2Bd}{12c} - s(a,k) %2B \frac{a%2Bd}{12k}

Then one has nδ is an even integer.

Rademacher's generalization of the reciprocity law

Hans Rademacher found the following generalization of the reciprocity law for Dedekind sums:[1] If a,b, and c are pairwise coprime positive integers, then

D(a,b;c)%2BD(b,c;a)%2BD(c,a;b)=\frac{1}{12}\frac{a^2%2Bb^2%2Bc^2}{abc}-\frac{1}{4}.

References

  1. ^ H. Rademacher, Generalization of the Reciprocity Formula for Dedekind Sums, Duke Mathematical Journal 21 (1954), pp. 391-397